フェルマーの最終定理について。これは数学史上、最も有名で、同時に多くの数学者を悩ませてきた定理の一つです。

フェルマーの最終定理とは?
17世紀のフランスの数学者ピエール・ド・フェルマーが、古代ギリシャの数学者ディオファントスの著書『算術』の余白に書き残したとされる有名なメモに端を発します。その内容は非常にシンプルです。
のとき、を満たす自然数 は存在しない。
つまり、我々がよく知っているピタゴラスの定理( の場合、 を満たす自然数、例えば が無限に存在します)の指数を2より大きくすると、整数解が存在しなくなる、という主張です。
フェルマーは余白に「私はこの定理の真に驚くべき証明を発見したが、この余白はそれを書くには狭すぎる」と書き残しました。この言葉が、その後の350年以上にわたる数学者たちの挑戦の始まりとなりました。
なぜ「最終定理」なのか?
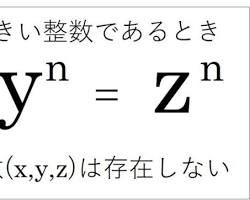
フェルマーが残した他の定理は、彼の死後、数学者たちによって次々と証明されていきました。しかし、この定理だけは最後まで証明されずに残ったため、「最終定理」と呼ばれるようになりました。
証明への長い道のり
多くの数学者がこの定理の証明に挑みましたが、誰も完全な証明を成し遂げられませんでした。特定の の値については証明されましたが、すべての について一般的に証明するのは極めて困難でした。
アンドリュー・ワイルズによる解決
そして、1994年、イギリスの数学者アンドリュー・ワイルズが、この350年以上もの間未解決だったフェルマーの最終定理の証明に成功しました。
ワイルズの証明は、谷山・志村予想(現在はモジュラー性定理の一部)という、一見フェルマーの最終定理とは無関係に見える楕円曲線とモジュラー形式に関する深い予想を足がかりに行われました。彼は7年もの間、この証明に没頭し、その間の研究成果をほとんど公表しませんでした。
ワイルズの証明は非常に高度で複雑であり、現代数学の様々な分野(数論、代数幾何学、楕円曲線論、モジュラー形式論など)の知識を総動員したものでした。彼は一度、証明に不備が見つかりましたが、共同研究者のリチャード・テイラーの協力も得て、その不備を修正し、最終的に完全な証明を完成させました。
フェルマーの最終定理の意義
フェルマーの最終定理は、それ自体が数学的に美しい主張であるだけでなく、その証明の過程で、数多くの新しい数学的概念や理論が生まれ、数学の発展に多大な貢献をしました。ワイルズによる証明は、20世紀の数学の集大成とも言える偉業であり、数学界に大きな衝撃と感動を与えました。